
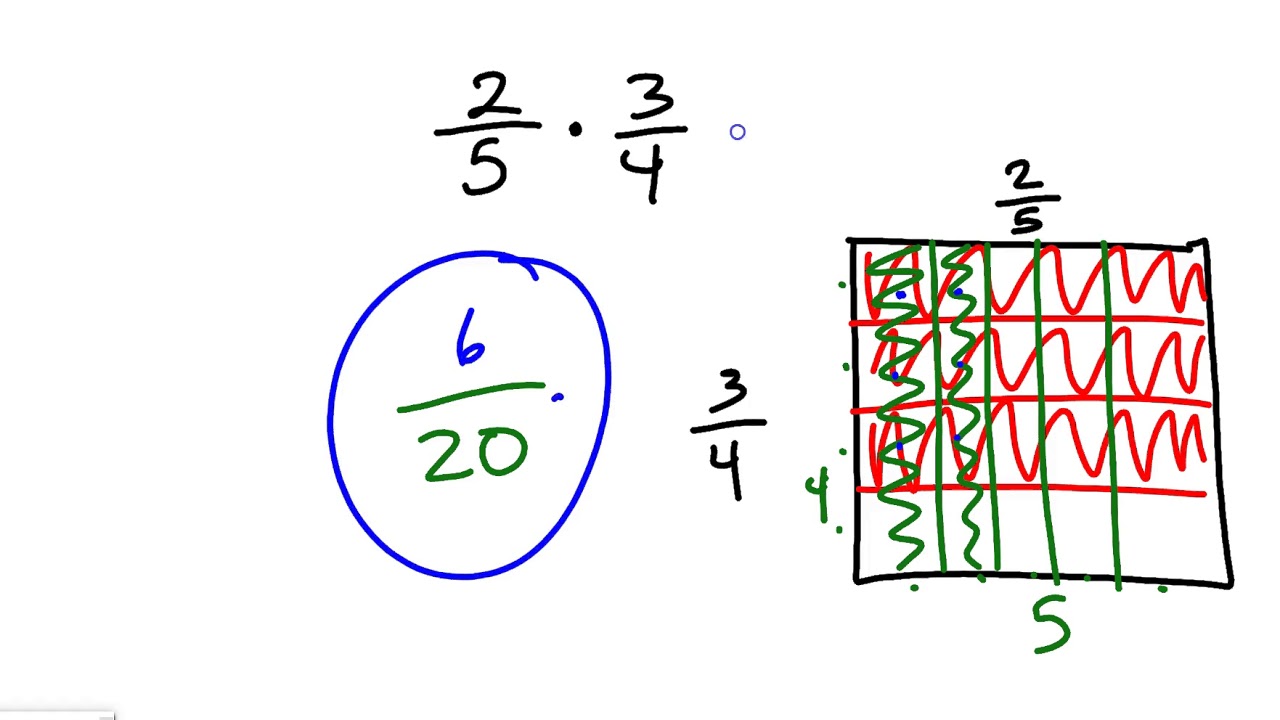
If we were to demonstrate 2/3 = 8/12 fact using an area model, first divide the area of the unit square into three rectangles. If your students are ready to be challenged with the symbolic form, you can explain: After various opportunities to experiment informally with fraction sticks and write down their observations, they will be ready to learn a more formal rule: when you multiply the numerator and denominator by the same non-zero number, you will obtain an equivalent fraction. They can choose a fraction, such as 2/3, and see what combinations of other fractions are equivalent, such as 8/12. This is a great time for students to experiment informally with fraction sticks.

So, let’s talk about finding equivalent fractions! Understanding equivalent fractions is important when comparing and ordering fractions, adding and subtracting fractions with unlike denominators, and reducing fractions to their lowest term. Here are some math concepts you can model with fraction sticks and area models:Ī prevalent theme in the Grade 4 Common Core standards is understanding equivalent fractions, or, more precisely, the notion that a fraction remains the same when you multiply the numerator and denominator by a non-zero whole number. An area model is a square that you divide into equal-sized rectangles to represent a fraction. An area model is a useful tool you can use to model certain fraction concepts.


 0 kommentar(er)
0 kommentar(er)
